प्रत्यावर्ती धारा सिद्धान्त:- विद्युत् शक्ति की आपूर्ति
दो प्रकार से की जाती है। 1. प्रत्यावर्ती धारा(A.C.), 2. दिष्ट धारा(D.C.)
प्रत्यावर्ती धारा(A.C.):- इसमें धारा प्रवाह
की दिशा हर समय बदलती रहती है तथा एक निश्चित समयान्तराल पर अपने पथ को दोहराती है।
D.C. की अपेक्षा A.C. के लाभ- 1. AC को एक स्थान
से दुसरे स्थान तक उच्च वोल्टता तथा निम्न धारा पर परेषित किया जाता है जिससे अपेक्षाकृत
पतले तार का प्रयोग किया जाता है जिससे पारेषण खर्च कम होता है
2. AC का उत्पादन उच्च वोल्टता पर किया जा सकता
है जबकि DC का उत्पादन केवल 650 वोल्ट तक ही किया जा सकता है
3. AC का वोल्टता परिवर्तन आसानी से किया जा सकता
है जबकि DC के वोल्टता परिवर्तन में अधिक उपकरण के साथ-साथ विद्युत् भी अधिक व्यय
होता है
4. AC मोटर व अन्य उपकरणों की संरचना, DC मोटर के
उपकरणों की अपेक्षा छोटे व सरल होते है
5. AC को DC में आसानी से परिवर्तित किया जा सकता
है जबकि DC को AC में बदलने के लिए अधिक खर्च करना पड़ता है
D.C. की अपेक्षा A.C. के दोष- 1. AC में
धारा प्रवाह की दिशा निरंतर बदलती रहती है इसी करण इससे विद्युत् चुम्बक
नही बनाये जा सकते है
2. AC में वोल्टता का मान DC की अपेक्षा अधिक
होता है वायरिंग आदि में उच्च सामर्थ्य वाले अचालक आवश्यक होते है
3. मानव, मशीनरी, भवनों आदि की सुरक्षा की दृष्टि
से भू-संयोजन आवश्यक होता है
4. AC से बहुत से कार्य जैसे धातु शोधन, बैटरी
चार्जिंग, इलेक्ट्रोनिक उपकरण के कार्य आदि नही किये जा सकते है
AC सम्बन्धी महत्वपूर्ण पद-
1. फ्रीक्वेन्सी- विद्युत् धारा द्वारा 1 सेकण्ड
में पूर्ण किये गये चक्रों की संख्या उसकी फ्रीक्वेन्सी कहलाती है
f = P.N/120
P = पोल्स की संख्या
N = रोटर की घूर्णन गति
2. चक्र(Cycle)- प्रत्यावर्ती धारा की दिशा के एक
पूर्ण परिवर्तन को चक्र कहते है
3. समय अंतराल- प्रत्यावर्ती धारा के एक चक्र को
पूर्ण करने में लगा समय, समय अंतराल कहलाता है
समय अंतराल (T) =
1/f
4. तात्कालिक मान- प्रत्यावर्ती विद्युत् धारा के
अथवा वोल्टता के किसी भी पल पर मान उसका तात्कालिक मान कहलाता है
5. शिखर मान- प्रत्यावर्ती विद्युत् धारा अथवा
वोल्टता का धन अथवा ऋण दिशा में अधिकतम मान ही उसका शिखर मान कहलाता है
6. आर एम एस मान(Root Mean Square Value) या R.M.S. मान- प्रत्यावर्ती विद्युत् धारा अथवा वोल्टता का मान प्रति क्षण परिवर्तित होता रहता है अतः मापन एवम गणनाओं में उसका प्रभावी मान ही प्रयोग किया जाता है जिसे RMS मान कहते है RMS मान ज्ञात करने के लिए AC के तात्कालिक मानों का वर्ग करके उनका औसत निकाला जाता है
Irms = 0.707 Imax
इसी प्रकार, Erms = 0.707 Emax
7. औसत मान- प्रत्यावर्ती विद्युत् धारा
अथवा वोल्टता के आधे चक्र में तात्कालिक मनो का औसत उसका औसत मान कहलाता है
Iave = (I1+I2+I3+I4.........In)/n
Irms = 0.637 Imax
इसी प्रकार, Eave =
0.637 Emax
8. पीक फैक्टर या क्रैस्ट फैक्टर- शिखर
मान और प्रभावी मान के अनुपात पीक फैक्टर कहलाता है
पीक
फैक्टर = शिखर मान / प्रभावी मान
=
Imax / Irms = 1.414
9. फॉर्म फैक्टर- प्रभावी मान और औसत मान
के अनुपात को फॉर्म फैक्टर कहते है
फॉर्म
फैक्टर = प्रभावी मान / औसत मान
=
Irms/ Iave = 0.707Imax/0.637 Imax = 1.11
10. फेज- प्रत्यावर्ती विद्युत् धारा अथवा
वोल्टता की दिशा निरंतर परिवर्तित होती रहती है अतः किसी भी पल उसकी दिशा ही उसकी
कला या फेज कहलाती है
11. इन-फेज- जब दो प्रत्यावर्ती राशियाँ
जैसे विद्युत् धारा एवं वोल्टता साथ-साथ बढ़ती-घटती हुई एक ही समय में अपने शिखर
मान पर पहुचती है तो वे इन-फेज राशियाँ कहलाती है
12. आउट-फेज- जब विद्युत् धारा एवं वोल्टता एक साथ अपने शिखर मान पर न पहुचकर कुछ आगे-पीछे पहुचती है तो वे आउट-फेज राशियाँ कहलाती है
13. लीडिंग तथा लैगिंग राशियाँ- वह
प्रत्यावर्ती राशि जो दूसरी राशि से पहले अपने शिखर मान पर पहुचें, लीडिंग राशि
कहलाती है इसी प्रकार जो राशि बाद में अपने शिखर मान पर पहुचें लैगिंग राशि कहलाती
है
14. विद्युत् धारा का वेग- विद्युत् धारा का
प्रवाह वेग 3x108 मी०/से० होता है इसी वेग पर प्रकाश तरंगे, उष्मीय
तरंगे एवं रेडियो तरंगे चलती है
V = f.λ
V = विद्युत धारा का वेग
f = फ्रीक्वेंसी
λ = तरंग दैर्ध्य
प्रेरकत्व(Inductance):- जब किसी चालक में AC विद्युत्
धारा प्रवाहित की जाती है तो उसमे एक विरोधी वि०वा०बल पैदा हो जाता है जो आरोपित
वि०वा०बल का विरोध करता है चालक का यह गुण उसका इन्डक्टैन्स कहलाता है
इन्डक्टैन्स का गुण केवल AC वैद्युत धारा के साथ पैदा होता है DC
धारा के सम्बन्ध में इन्डक्शन प्रभाव पैदा नही होता है
एक हैनरी- यदि किसी
कुण्डली में 1 एम्पियर प्रति सेकण्ड की दर पर विद्युत् धारा के परिवर्तन से 1
वोल्ट का वि०वा०बल पैदा होता है तो उस कुण्डली का इन्डक्टैन्स 1 हैनरी होगा
1 हैनरी = 1 वोल्ट / 1 कुलॉम
एक अन्य सूत्र, हैनरी (L) = N.
Φ/I
N = कुण्डली की लपेट संख्या
Φ = कुण्डली में से गुजरने वाला चुम्बकीय फ्लक्स
I = कुण्डली में प्रवाहित विद्युत् धारा
प्रेरकत्व दो
प्रकार के होते है
1. स्व प्रेरकत्व(Self Inductance):- जब कुण्डली में विद्युत्
धारा प्रवाहित की जाती हो और उसी कुण्डली में विरोधी वि०वा०बल पैदा होता है तो उसे
स्व प्रेरकत्व कहते है
2. अन्योन्य प्रेरण(Mutual Inductance):- जब कुण्डली में विद्युत्
धारा प्रवाहित की जाती हो और उसके द्वारा स्थापित चुम्बकीय क्षेत्र में किसी दूसरी
कुण्डली में विरोधी वि०वा०बल पैदा होता है तो उसे अन्योन्य प्रेरण कहते है
अन्योन्य प्रेरण(M) = √(L1.L2)
L1 = प्रथम कुण्डली का सैल्फ इन्डक्टैन्स
L2 = दूसरी कुण्डली का सैल्फ इन्डक्टैन्स
प्रेरण का समूहन- प्रतिरोध की भॉति इन्डक्टर्स को भी
आवश्यकतानुसार श्रेणी एवं समान्तर क्रम में संयोजित किया जा सकता है
श्रेणी क्रम- LT =L1+L2+L3+..........Ln
समान्तर क्रम- 1/LT = 1/L1+1/L2+1/L3+..........1/Ln
इन्डक्टिव रिएक्टैन्स:- किसी भी चालक अथवा कुण्डली
में इन्डक्टैन्स विद्यमान होता है जिसके करण चालक अथवा कुण्डली में प्रत्यावर्ती
विद्युत् धारा के प्रवाह का विरोध होता है इसी होने वाले विरोध को ही इन्डक्टिव
रिएक्टैन्स कहते है
या प्रत्यावर्ती विद्युत् धारा प्रवाह के लिए किसी कुण्डली
द्वारा प्रस्तुत किया जाने वाला विरोध ही उसका इन्डक्टिव रिएक्टैन्स कहलाता है इसे
XL से दर्शाते है इसका मात्रक Ω(ओह्म) होता है
XL = 2 πfL = V∕IL
f = फ्रीक्वेंसी
L = इन्डक्टैन्स
शुद्ध इन्डक्टिव परिपथ:- इस प्रकार के परिपथ में विद्युत् धारा, वि०वा०बल से 90० पीछे रहती है क्योंकि जैसे ही परिपथ में वि०वा०बल क्रियाशील होता है विरोधी वि०वा०बल भी पैदा हो जाता है और विद्युत् धारा प्रवाहित नही हो पाती है और जब वि०वा०बल अपने अधिकतम मान पर पहुचकर फिर कम होने लगता है तो विरोधी वि०वा०बल भी घटने लगता है जिससे विद्युत् धारा प्रवाहित होने लगता है इस प्रकार विद्युत् धारा वि०वा०बल से 90० पिछड़ जाता है
वास्तव में कोई परिपथ शुद्ध
इन्डक्टिव नही होता है क्योंकि प्रत्येक इन्डक्टर तथा उसके संयोजक तार में कुछ न
कुछ प्रतिरोध अवश्य होता है इसलिए विद्युत् धारा कभी भी वि०वा०बल से 90०
पीछे नही रह सकता है शुद्ध इन्डक्टिव परिपथ में प्रतिरोध (R) का मान शून्य होता है
धारिता(Capacitance):- A.C. परिपथ का वह गुण जिसके
कारण वह वोल्टता मान में होने वाले परिवर्तनों का विरोध करता है संधारकत्व या
धारिता कहलाता है इसका प्रतिक C तथा मात्रक फैरड(F) होता है
संधारित्र(Capacitor या
Condensor):- किसी अचालक पदार्थ से अलग की गयी डी चालक प्लेटों से निर्मित ऐसी
युक्ति जो वैद्युतिक आवेश एकत्रित कर सके संधारित्र कहलाती है
संधारित्र का उपयोग क्षणिक
विद्युत् धारा प्राप्त करने के लिए किया जाता है
संधारित्र के प्रकार-
1. कार्य के आधार पर-
1. नियत मान संधारित्र,
2. समायोजनीय मान संधारित्र,
3. परिवर्तनीय मान संधारित्र
2. अचालक के
आधार पर-
1. पेपर संधारित्र,
2. माइका संधारित्र,
3. सेरामिक संधारित्र
4. इलेक्ट्रोलाइट संधारित्र
5. ऑयल डाइ-इलेक्ट्रिक
संधारित्र
संधारित्र का उपयोग मोटर,
ट्यूब-लाइट, सोडियम लैंप, पंखा तथा अन्य इलेक्ट्रोनिक युक्तियों में किया जाता है
समान्तर प्लेट संधारित्र के
धारिता की गणना का सूत्र-
C = 8.85 KA(N-1)
C = धारिता
K = अचालक नियतांक
A = एक प्लेट का क्षेत्रफल
t = अचालक की मोटाई
N = प्लेटों की संख्या
संधारित्र का समूहन:-
1. समान्तर क्रम में- इसमें सभी संधारित्र एक ही
श्रोत वोल्टता से जुड़े रहते है अतः कुल परिणामी आवेश,
QT = Q1 + Q2 + Q3.................
यहां Q = CV
अतः CTV = C1V
+ C2V + C3V...................
C1 + C2 + C3..................
2. श्रेणी क्रम में- इसमें श्रोत वोल्टता, सभी
संधारित्र के धारिता के मान के अनुसार वितरित हो जाता है अतः
VT = V1 + V2 + V3.................
यहां V = Q/C
अतः Q/CT = Q/C1
+ Q/C2 + Q/C3...................
1/CT = 1/C1 + 1/C2 + 1/C3..................
कैपेसिटिव रिएक्टैन्स:- प्रत्येक संधारित्र की कुछ न
कुछ धारिता अवश्य होती है जिसके करण वह अपने सिरों पर आरोपित वोल्टता के
परिवर्तनों का विरोध करती है अतः
प्रत्यावर्ती विद्युत् धारा प्रवाह के लिए किसी संधारित्र द्वारा
प्रस्तुत किया जाने वाला विरोध ही उसका कैपेसिटिव रिएक्टैन्स कहलाता है इसका
प्रतिक Xc तथा मात्रक Ω(ओह्म) होता है
Xc = 1/2πfC
f = फ्रीक्वेंसी
C = धारिता, फैरड में
परिपथ
में विद्युत् धारा (I) = V/Xc (V = वोल्टता)
शुद्ध कैपेसिटिव परिपथ:- केवल संधारित्र युक्त A.C. परिपथ, शुद्ध कैपेसिटिव परिपथ कहलाती है इस परिपथ में वोल्टता, विद्युत् धारा से 90० पिछड़ जाती है क्योंकि जब परिपथ को A.C. श्रोत से जोड़ा जाता है तो संधारित्र को आवेशित करने के लिए अधिक संख्या में इलेक्ट्रॉन्स संधारित्र की प्लेट पर पहुचते है जिससे विद्युत् धारा का प्रारम्भिक मान अधिकतम होता है तथा वोल्टता का मान शून्य होता है जैसे-जैसे संधारित्र आवेशित होता जाता है विद्युत् धारा का मान घटता जाता है तथा वोल्टता का मान बढ़ता जाता है शुद्ध कैपेसिटिव परिपथ का शक्ति व्यय शून्य होता है
इम्पीडेन्स(Impedance):- प्रत्येक A.C. परिपथ में इन्डक्टैन्स,
कैपेसिटेन्स तथा प्रतिरोध तीनों कुछ न कुछ अवश्य होते है अतः किसी AC परिपथ में
विद्युत् धारा प्रवाह के लिए विद्यमान कुल अवरोध, इम्पीडेन्स कहलाती है इसका
प्रतिरोध Z तथा मात्रक Ω होता
है
1. श्रेणी R-L परिपथ- इस परिपथ में प्रतिरोधक तथा इन्डक्टर श्रेणी क्रम में संयोजित होते है। R, परिपथ के कुल प्रतिरोध को दर्शाता है
इस
परिपथ में विद्युत् धारा के वोल्टता से पिछड़ने के कोण का मान 90० से कम
होता है cos Φ का मान प्रतिरोध R पर निर्भर होता
है
ΔOAR से परिपथ
का इम्पीडेन्स,
V2 = (VR)2 + (VL)2
V2 = I2R2 + I2(XL)2
V2/ I2 = R2 + (XL)2 = Z2
या Z
= √(R2 + (XL)2
)
तथा पॉवर
फैक्टर (cos Φ) = R∕Z
एवं व्यय
शक्ति P = VI.cos Φ
2. श्रेणी R-C परिपथ- इसमें प्रतिरोध तथा संधारित्र श्रेणी क्रम में जुड़े होते है R, परिपथ में जुड़े प्रतिरोध, संधारित्र एवं संयोजक तारों के प्रतिरोध(कुल प्रतिरोध) को दर्शाता है इस परिपथ में विद्युत् धारा के वोल्टता से आगे बढ़ने के कोण का मान 90० से कम होता है
V2 = (VR)2 + (VC)2
V2 = I2R2 + I2(XC)2
V2/ I2 = R2 + (XC)2 = Z2
या Z
= √(R2 + (XC)2
)
तथा पॉवर
फैक्टर (cos Φ) = R∕Z
एवं व्यय
शक्ति P = VI.cos Φ
3. श्रेणी R-L-C परिपथ- इस परिपथ में प्रतिरोधक, इन्डक्टर तथा संधारित्र तीनों श्रेणी क्रम में जुड़े होते है इस परिपथ की परिणामी वोल्टता तथा विद्युत् धारा के वोल्टता से पिछड़ने अथवा आगे बढ़ने के कोण का मान निम्नवत होता है
V2
= (VR)2 + (VL ~VC)2
V2
= I2R2
+ I2(XL~XC)2
V2/ I2 = R2 + (XL~XC)2
= Z2
या Z
= √(R2 + (XL~XC)2
)
तथा पॉवर
फैक्टर (cos Φ) = R∕Z
एवं व्यय
शक्ति P = VI.cos Φ
फेज अंतर tan Φ = (XL~XC)∕R
पॉवर
फैक्टर- A.C. परिपथ में वास्तविक शक्ति एवं
आभासी शक्ति का अनुपात पॉवर फैक्टर कहलाता है
पॉवर
फैक्टर (P.F.) = वास्तविक शक्ति∕ आभासी शक्ति
= VI.cos Φ∕VI
P.F. = cos Φ = R∕Z














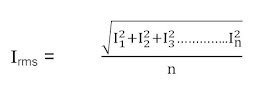



.JPG)
















0 comments:
Post a Comment